Uge 9a: Kurve- og fladeintegraler af skalære funktioner

Demo af Christian Mikkelstrup, Hans Henrik Hermansen, Jakob Lemvig, Karl Johan Måstrup Kristensen og Magnus Troen

from sympy import *
from dtumathtools import*
init_printing()
x,y,z = symbols('x y z', real=True)

Kurvelængder

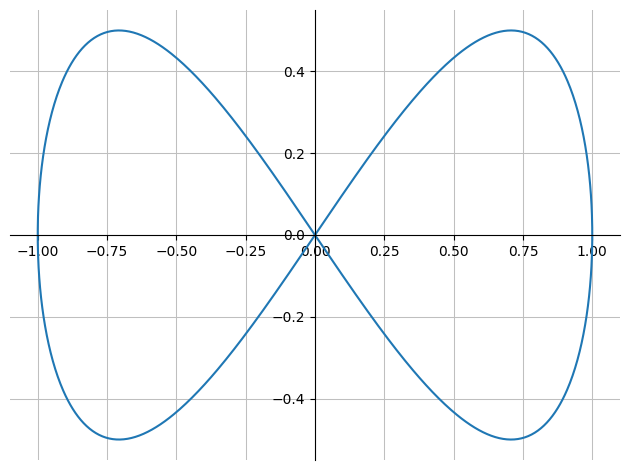
Vi får givet en parameter-kurve,

u,v = symbols('u v', real=True)
r = Matrix([sin(u), sin(u)*cos(u)])
r

\[\begin{split}\displaystyle \left[\begin{matrix}\sin{\left(u \right)}\\\sin{\left(u \right)} \cos{\left(u \right)}\end{matrix}\right]\end{split}\]

hvor \(u \in [0, 2\pi]\)

p_kurve = dtuplot.plot_parametric(*r, (u,0,2*pi), use_cm=False, label="r(u)",axis_center="auto")

Tangentvektor og tangent

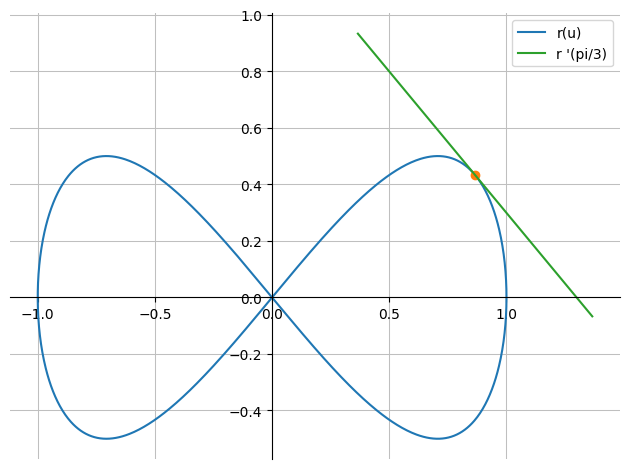
Vi finder tangentvektoren,

dr = r.diff(u)
dr

\[\begin{split}\displaystyle \left[\begin{matrix}\cos{\left(u \right)}\\- \sin^{2}{\left(u \right)} + \cos^{2}{\left(u \right)}\end{matrix}\right]\end{split}\]

Vi finder nu parameterfremstillingen for tangenten svarende til kurvepunktet \(r(\pi/3)\),

t = symbols("t")
r_tan = r.subs(u,pi/3) + t*dr.subs(u,pi/3)
r_tan

\[\begin{split}\displaystyle \left[\begin{matrix}\frac{t}{2} + \frac{\sqrt{3}}{2}\\- \frac{t}{2} + \frac{\sqrt{3}}{4}\end{matrix}\right]\end{split}\]

p_point = dtuplot.scatter(r.subs(u,pi/3), show=False)
p_tan = dtuplot.plot_parametric(*r_tan, (t,-1,1), use_cm=False, label="r '(pi/3)", show=False)


(p_kurve + p_point + p_tan).show()

Længden af kurven

Og så kan længden af denne kurve findes ved

\[\begin{equation*} \int_K\; \mathrm{d}\pmb{s} = \int_{0}^{2\pi} \Vert r'(u) \Vert \mathrm{d}u \end{equation*}\]

jacobiant = dtutools.l2_norm(dr)
integrate(jacobiant, (u,0,2*pi)).n()

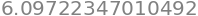
Kurveintegral i rummet

Vi får givet en funktion:

x,y,z = symbols("x y z")
f = lambda x,y,z: sqrt(x**2 + y**2 + z**2)
f(x,y,z)

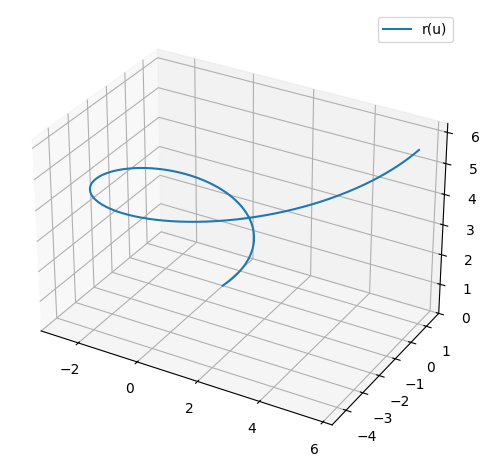
og en parameterkurve

r = Matrix([u*cos(u), u*sin(u), u])
r

\[\begin{split}\displaystyle \left[\begin{matrix}u \cos{\left(u \right)}\\u \sin{\left(u \right)}\\u\end{matrix}\right]\end{split}\]

for \(u\in[0,5]\).

p_rumkurve = dtuplot.plot3d_parametric_line(*r, (u,0,2*pi), use_cm=False, label="r(u)",aspect="equal", legend=True)

Restriktionen af funktionen til kurven er:

begrænsning = f(*r).simplify()
begrænsning

og hvis man husker at \(u\) er positiv, da vi har defineret \(u\in [0, 5]\), er absolutværdien irrelevant. Vi har dog, ved definitionen af vores u og v, defineret dem ved

u,v = symbols('u v', real=True)

hvor SymPy kun tager højde for at \(u=|u|\) i lige præcis det her tilfælde, hvis vi havde defineret dem ved

u,v = symbols('u v', real=True, nonnegative=True)

i stedet kan vi nu bruge \(\verb|refine()|\) og \(\verb|Q.|\textit{assumption}\verb|(symbol)|\), hvor assumption kan skiftes ud med prædikaterne i denne tabel.

Vi skal her bruge \(\verb|Q.nonnegative()|\), og så viser SymPy at begrænsningen faktisk er

ægte_begrænsning = refine(begrænsning, Q.nonnegative(u)) # Q.nonnegative(u) fortæller refine() at u >= 0
ægte_begrænsning

for \(u \in [0,5]\). Hvorvidt der står \(u\) eller \(|u|\) i udtrykket, kan nogen gange gøre forskellen hvis SymPy prøver integrerer det

Tilbage til kurveintegralet vi ønsker at bestemme: \(\int_K f(x,y,z)\, \mathrm{d}\pmb{s}\).

Først finder vi tangentvektoren,

dr = r.diff(u)
dr

\[\begin{split}\displaystyle \left[\begin{matrix}- u \sin{\left(u \right)} + \cos{\left(u \right)}\\u \cos{\left(u \right)} + \sin{\left(u \right)}\\1\end{matrix}\right]\end{split}\]

Længden af tangentvektoren \(||r_u'(u)||\) er lig med jacobianten,

jacobiant = dtutools.l2_norm(dr).simplify()

# Følgende linje virker kun hvis $u$ er en reel variabel
# altså hvis 'u = symbols('u', real=True)'
# jacobi = dr.norm()

jacobiant

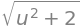
Vi kan nu finde integralet langs kurven,

integrate( f(*r) * jacobiant ,(u,0,5)).evalf()

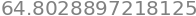
og kurvens længde,

integrate(jacobiant,(u,0,5)).evalf()

Integral over cylinderflade i \(\mathbb{R}^3\)

Vi betragter en funktion \(f: \mathbb{R}^3 \to \mathbb{R}\) givet ved

\[\begin{equation*} f(x,y,z) = 8 z \end{equation*}\]

Vi betragter også en flade givet ved følgende parameterfremstilling med \(u \in [0,\frac{\pi}{2}]\) og \(v \in [0,1]\)

# Denne gang husker vi 'nonnegative=True', da vi igen ser at
# ingen af intervallerne for u og v indeholder negative tal
u,v = symbols('u v', real=True, nonnegative=True)
r = Matrix([u*cos(u),u*sin(u),u*v])

def f(x,y,z):
    return 8*z

r, f(x,y,z)

\[\begin{split}\displaystyle \left( \left[\begin{matrix}u \cos{\left(u \right)}\\u \sin{\left(u \right)}\\u v\end{matrix}\right], \ 8 z\right)\end{split}\]

dtuplot.plot3d_parametric_surface(*r,(u,0,pi/2),(v,0,1), aspect='equal')

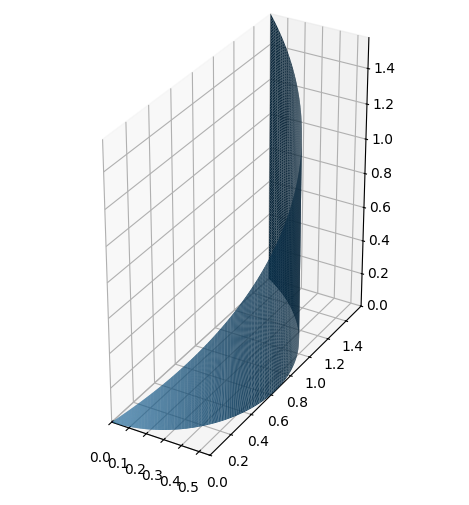
<spb.backends.matplotlib.matplotlib.MatplotlibBackend at 0x7f92f96dde50>

Jacobianten for en flade i 3D

Vi finder jacobianten og indsætter parameterfremstillingen i \(f\)

kryds = r.diff(u).cross(r.diff(v))
jacobianten = sqrt((kryds.T * kryds)[0]).simplify()
jacobianten

integrand = f(*r) * jacobianten
integrand

integrate(integrand,(v,0,1),(u,0,pi/2)).evalf()