Uge 1: Forberedelse#
Læsestof#
Vi anbefaler at du læser i bogen. At se YouTube-videoer om ugens emner kan være nyttigt, men det er ikke noget vi specielt anbefaler, og det bør ikke træde i stedet for egentlig forberedelse til ugens program.
Du skal læse og studere:
Repetition: Studér Kapitel 0
Store Dag: Kapitel 1, Afsnit 2.1, Afsnit 3.1 og Afsnit 3.2
Lille Dag: Afsnit 2.2, Afsnit 3.2 og Afsnit 3.3
Python demo
Nøglebegreber#
Når du har læst bør du kunne forklare følgende nøglebegreber:
Skalarfunktioner: specielt kvadratiske former
Vektorfunktioner
Visualisering af funktioner: Grafer og niveaukurver/mængder
Kontinuitet
Det sædvanlige indreprodukt (prikproduktet) og norm i \(\mathbb{R}^n\)
Partielle afledte og Gradientvektoren
I ugens program arbejder vi videre med nøglebegreberne – vi forventer altså ikke at du kender alle detaljer om disse begreber, men vi forventer at du har stiftet bekendtskab med dem inden forelæsning.
Forberedelsesopgaver#
I: Funktionsværdien i et punkt#
Spørgsmål a#
Indsæt værdierne \(x = 2\) og \(y = -1\) i funktionsudtrykket \(f(x, y) = x^2 + 3xy + 4y^2\) og beregn \(f(2, -1)\).
Hint
Erstat \(x\) med \(2\) og \(y\) med \(-1\) i udtrykket \(x^2 + 3xy + 4 y^2\).
Svar
\(f(2, -1) = 2^2 + 3(2)(-1) + 4(-1)^2 = 4 - 6 + 4 = 2\)
Spørgsmål b#
Lad \(g: \mathbb{R}^2 \to \mathbb{R}\) være givet ved funktionsudtrykket \(g(x_1, x_2) = x_1^2 + 3x_1 x_2 + 4 x_2^2\). Beregn \(g(2, -1)\).
Hint
Det er samme funktionsudtryk som i forrige opgave, så fremgangsmåde og svar er det samme.
Spørgsmål c#
Lad \(\alpha \in \mathbb{R}\). Find \(g(2 \alpha, \alpha)\) og \(g(\alpha, 2 \alpha)\), hvor \(g\) er defineret i forrige opgave. Udregn den afledte af \(g(2 \alpha, \alpha)\) med hensyn til \(\alpha\).
Hint
For \(g(2 \alpha, \alpha)\), indsæt \(x_1 = 2 \alpha\) og \(x_2 = \alpha\) i \(g(x_1, x_2) = x_1^2 + 3x_1x_2 + 4x_2^2\). Gentag for \(g(\alpha, 2 \alpha)\). For den afledte skal du differentiere udtrykket for \(g(2 \alpha, \alpha)\) mht \(\alpha\).
Svar
Ved indsættelse fås: \(g(2 \alpha, \alpha) = (2\alpha)^2 + 3(2 \alpha)(\alpha) + 4(\alpha)^2 = (4+6+4)\alpha^2 = 14 \alpha^2\) og \(g(\alpha, 2\alpha) = (\alpha)^2 + 3(\alpha)(2\alpha) + 4(2\alpha)^2 = (1+6+16) \alpha^2 = 23 \alpha^2\).
Den afledte af \(g(2 \alpha, \alpha)= 14 \alpha^2\) med hensyn til \(\alpha\) er \(\frac{d}{d\alpha} \big( 14 \alpha^2 \big) = 28 \alpha = 28 \alpha\).
II: Niveaukurver#
Beskriv niveaukurverne (contour lines) for funktionen \(f: \mathbb{R}^2 \to \mathbb{R}\) givet ved \(f(x, y) = x^2 + y^2 - 5\).
Hint
Brug fx Python. Niveaukurven for \(f(x, y) = 9\) kan fx plottes ved:
x, y = symbols("x y", real=True)
f = x**2 + y**2 - 5
dtuplot.plot_implicit(Eq(f,9), (x,-10,10), (y,-10,10))
III: Graf eller niveau-kurve?#
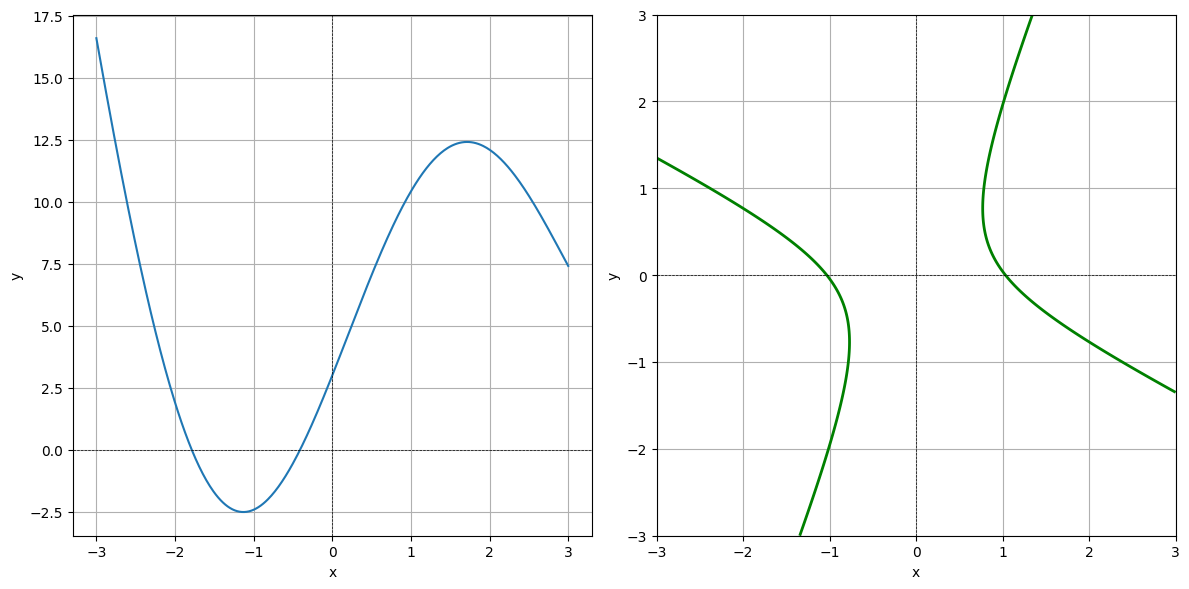
Nedenfor vises grafen af en funktion \(f_1\) af en variable og en niveaukurve af en funktion \(f_2\) af to variable. Hvilket plot er grafen og hvilet plot er niveaukurven?
IV: Diskontinuert i ét punkt#
Tegn, beskriv eller definér en funktion \(h: \mathbb{R} \to \mathbb{R}\), der er kontinuert i alle punkter undtagen et enkelt punkt.
Svar
En mulig funktion er \(h(x) = \begin{cases} x & \text{hvis } x \neq 1 \\ 0 & \text{hvis } x = 1 \end{cases}\). Denne funktion er kontinuert overalt undtagen i \(x = 1\).

