Uge 1: Afrunding

Uge 1: Afrunding#

Arbejd videre med opgaverne fra forberedelsen og øvelserne, som du endnu ikke har løst.

Nøglebegreber#

  • Skalar-funktioner: specielt kvadratiske former

  • Vektor-funktioner

  • Visualisering af funktioner: Grafer og niveaukurver/mængder

  • Kontinuitet

  • Det sædvanlige indreprodukt (prikproduktet) og norm i \(\mathbb{R}^n\)

  • Partielle afledte og Gradientvektoren

Hvis der stadig er begreber du er usikker på hvad dækker over, bør du genlæse ugens tekst eller genregne ugens øvelsesopgaver.

Ekstra opgaver#

Vi forventer ikke at du laver flere opgaver end øvelsesopgaverne fra ugens program. De følgende ekstraopgaver er udelukkende et frivilligt tilbud for dem, der ønsker yderligere træning og udfordring.

1: Visualiseringer - tur på et bjerg#

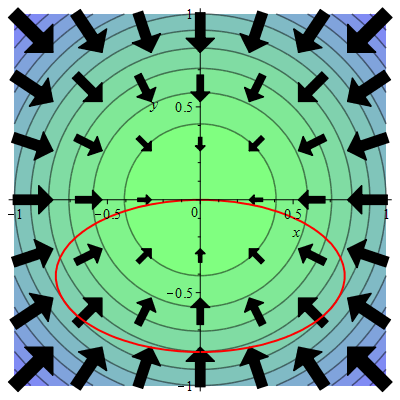
Vi ser på et højdekort for et bjerg, hvor cirklerne er niveaukurver for højdefunktionen. Pilene angiver højdefunktionens gradientvektorfelt. På bjerget findes en elliptisk vandresti som på kortet er rød. Bjerg

Spørgsmål a#

Forestil dig du går en tur langs den røde sti i positiv omløbsretning (mod uret). Find de punkter på stien hvor stigningen er 0 (det går hverken opad eller nedad).

Hint

Der er fire steder.

Svar

På en niveaukurve ændres højden selvfølgelig ikke. Derfor gælder det om at finde de steder på stien hvor stien har fælles tangent med en niveaukurve.

Spørgsmål b#

På hvilke stykker af stien går det opad, og på hvilke nedad?

Spørgsmål c#

Følg nu en af niveaukurverne på tegningen hele vejen rundt og betragt retningen af de gradientvektorer der ligger lige i nærheden. Konklusion?

Spørgsmål d#

Dette bjerg er selvfølgelig ret specielt. Men tag igen vandrestøvlerne på, og giv et intuitivt argument for hvorfor gradientvektorerne altid, på alle bjerge, må være vinkelrette på niveaukurverne?

Svar

Forslag: Hvis vi betragter niveaukurven som en sti vi spadserer ad, er turen stille og rolig. Vi går nemlig hele tiden vandret. Det forekommer naturligt at stigningen må være størst hvis vi brat ændrer retningen med 90 grader opad. Enig?

2: Kontinuitet af førstegradspolynomier#

Bevis at polynomiumsfunktionen \(f : \mathbb{R} \to \mathbb{R}\), \(f(x)=3x\) er kontinuert i alle punkter \(x \in \mathbb{R}\).

Hint

Brug \(\epsilon-\delta\) definitionen. Se denne ligning i noten.

Hint

Lad \(x_0\) være et vilkårligt reelt tal, og lad \(\epsilon > 0\) være givet. Du skal nu angive hvordan man kan vælge \(\delta > 0\) (det må gerne afhænge af \(x_0\) og \(\epsilon\)) så \( |x-x_0| < \delta \Rightarrow |f(x)-f(x_0)| < \epsilon\).

3: Grænseovergang af en funktion \(f: \mathbb{R}^2 \to \mathbb{R}\)#

Lad \(f: \mathbb{R}^2 \to \mathbb{R}\) være givet ved:

\[\begin{equation*} f(x,y) = \begin{cases} \displaystyle \frac{x\,y + x^3 + xy^2}{x^2 + y^2} & \text{hvis } (x,y)\neq (0,0),\\ 0, & \text{hvis } (x,y) = (0,0). \end{cases} \end{equation*}\]

Spørgsmål a#

Find \(f(x, x)\) for \(x \neq 0\). Find dernæst \(f(y, y)\) for \(y \neq 0\).

Hint

Indsæt \(y = x\) i funktionsudtrykket for \(f(x,y)\). Husk at forenkle brøken.

Hint

Når du har fundet \(f(x, x)\), kan \(f(y, y)\) findes ved blot at erstatte \(x\) med \(y\). Der er jo tale om samme udtryk, blot med forskellig benævnelse af den variable.

Svar

For \(x \neq 0\):

\[\begin{equation*} f(x,x) \;=\; \frac{x\,x + x^3 + xx^2}{x^2 + x^2} \;=\; \frac{x^2}{2x^2} + \frac{2x^3}{2x^2} \;=\; \tfrac12 + x. \end{equation*}\]

Spørgsmål b#

Bestem \(\lim_{x \to 0} f(x,x)\).

Svar

Af udtrykket i forrige opgave fås:

\[\begin{equation*} \lim_{x \to 0} f(x,x) \;=\; \lim_{x\to 0} \Bigl(\tfrac12 + x\Bigr) \;=\; \tfrac12. \end{equation*}\]

Spørgsmål c#

Bestem \( \lim_{x \to 0} f(x,2x) \).

Hint

Indsæt \( y = 2x \) i formlen for \(f(x,y)\) og reducer udtrykket.

Svar

For \( x \neq 0 \) fås \(f(x,2x) \;=\; \tfrac{2}{5} + x\) og derfor

\[\begin{equation*} \lim_{x \to 0} f(x,2x) \;=\; \lim_{x\to 0} \Bigl(\tfrac{2}{5} + x\Bigr) \;=\; \tfrac{2}{5}. \end{equation*}\]

Spørgsmål d#

Overvej om grænseværdien \(\lim_{(x,y)\to (0,0)} f(x,y)\) eksisterer.

Svar

Når vi nærmer os \((0,0)\) langs linjerne \(y=x\) and \(y=2x\), finder vi to forskellige værdier. Da grænseværdien afhænger af vejen, eksisterer \( \lim_{(x,y)\to (0,0)} f(x,y)\) ikke. Dette viser at \(f\) ikke er kontinuert i \((0,0)\) (selv hvis vi fik lov til at ændre funktionsværdien \(f(0,0)\)).

Contents