Solution of Test Exam (F24)#
Suggested Solutions for test exam in 01002/01004 Mathematics 1b, F24.
By shsp@dtu.dk, 05/05-2024
from sympy import *
from dtumathtools import *
init_printing()
Exercise 1#
We are given the two partial derivatives, so the following gradient, of a function
x, y = symbols("x y")
fx = 6 * x - 6 * y
fy = 6 * y**2 - 6 * x
fx, fy

(a)#
Setting them equal to zero and solving for all solutions results in all stationary points:
statpt = solve([Eq(fx, 0), Eq(fy, 0)])
statpt

So,
(b)#
Second-order partial derivatives:
fxx = diff(fx, x)
fxy = diff(fx, y)
fyx = diff(fy, x)
fyy = diff(fy, y)
fxx, fxy, fyx, fyy

We see that the two partial mixed double derivatives are equal. Since
The Hessian matrix
H = Lambda(tuple([x, y]), Matrix([[fxx, fxy], [fyx, fyy]]))
H(x, y)
With no boundary given, extrema can only be found at stationary points or execptional points. Since
H(0, 0).eigenvals()
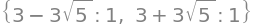
The eigenvalues have different signs, so according to Theorem 5.2.4,
lambdas = H(1, 1).eigenvals(multiple=True)
lambdas[0].evalf(), lambdas[1].evalf()

The eigenvalues are both positive, indicating a local minimum at
There are no more possible extremum points, so
(c)#
We are now informed that
Setting up the approximation:
Exercise 2#
A function
(a)#
3rd-degree Taylor polynomial of
sin(x).series(x, 0, 4)
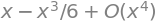
So, the Taylor polynomial of degree 3 is
P3 = x - x**3 / 6
P3, sin(x).series(x, 0, 4).removeO()

(b)#
The Taylor expansion (Taylor’s limit formula) of
where
We find the following limit value:
(c)#
According to remark to theorem 3.1.1 in the note,
(d)#
Defining the function for
def f(x):
return sin(x) / x
f(x)
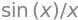
Computing a decimal approximation of
integrate(f(x), (x, 0, 1)).evalf()
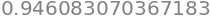
(e)#
We will compute a Riemann sum as an approximation of the area under the graph of
j = symbols("j")
delta_xj = 1 / 30
J = 30
xj = j / J
Sum(f(xj) * delta_xj, (j, 1, 30)).evalf()
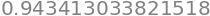
Alternatively, using at for loop:
riemann_sum = 0
N = 30
for i in range(1, N + 1):
riemann_sum += sin(i / N) / (i / N) * 1 / N
riemann_sum
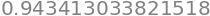
(f)#
Computing
integrate(P3, (x, 0, 1)).evalf()
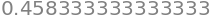
This approximation of the integral is worse than the approximation using a Riemann sum in the previous question, since a Taylor polynomial of
integrate(P3 / x, (x, 0, 1)).evalf()
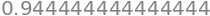
Exercise 3#
Given matrix
t = symbols("t")
Ct = Matrix([[1, 2, 3, 4], [4, 1, 2, 3], [3, 4, 1, 2], [t, 3, 4, 1]])
Ct
(a)#
The unitary matrix
Ct_uni = Ct.T
Ct_uni
Ct_uni * Ct
Ct * Ct_uni
solve(Eq(Ct * Ct_uni, Ct_uni * Ct))

So, only for
(b) and (c)#
Defining
A = Ct.subs(t, 2)
A
Given eigenvectors:
v1 = Matrix([1, 1, 1, 1])
v2 = Matrix([1, I, -1, -I])
Treating
A * v1, A * v2
From this we read the scaling factors, which are the eigenvalues corresponding to the given eigenvectors, to be
lambda1 = 10
lambda2 = -2 - 2 * I
Check:
A * v1 == lambda1 * v1, A * v2 == simplify(lambda2 * v2)
(True, True)
(d)#
Orthogonality is equivalent to an inner product of zero. The inner product of two complex vectors from
v1.dot(v2.conjugate())

We conclude that they are orthogonal,
(e)#
The norm is the root of the inner product of a vector with itself, e.g.
sqrt(v1.dot(v1))
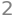
sqrt(v2.dot(v2.conjugate()))
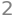
As their norms are not 1, they are not normalized. The list
Exercise 4#
Given quadratic form
def q(x1, x2):
return 2 * x1**2 - 2 * x1 * x2 + 2 * x2**2 - 4 * x1 + 2 * x2 + 2
x1, x2 = symbols("x1,x2")
q(x1, x2)
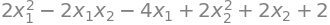
(a)#
For rewriting to matrix form
A = Matrix([[2, -1], [-1, 2]])
b = Matrix([-4, 2])
c = 2
A, b, c
Checking:
x = Matrix([x1, x2])
simplify(list(x.T * A * x + x.T * b)[0] + c)
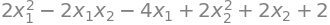
simplify(list(x.T * A * x + x.T * b)[0] + c) == q(x1, x2)
True
(b)#
We will now reduce the quadratic form
A.eigenvects()
v1 = Matrix([1, 1])
v2 = Matrix([-1, 1])
v1, v2
Also,
lambda1 = 1
lambda2 = 3
lambda1, lambda2

Since
q1 = v1.normalized()
q2 = v2.normalized()
q1, q2
A change-of-basis matrix
Q = Matrix.hstack(q1, q2)
Q
This can also be found directly by
Qmat, Lamda = A.diagonalize(normalize=True)
Qmat
(c)#
The new coordinates
k1, k2 = symbols("k1 k2")
k = Matrix([k1, k2])
k
In the new coordinates, the squared terms have coefficients equal to the eigenvalues of
q1 = lambda1 * k1**2 + lambda2 * k2**2 + list(k.T * Q.T * b)[0] + c
q1
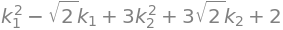
Check:
simplify(list(k.T * Q.T * A * Q * k + k.T * Q.T * b)[0] + c)
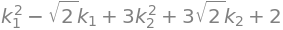
Factorizing by completing the square gives us the following suggestions to the constants:
alpha = 1
gamma = sqrt(2) / 2
beta = 3
delta = -sqrt(2) / 2
alpha, gamma, beta, delta
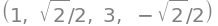
Setting up the suggested factorized form of
q1_fact = (
alpha * (k1 - gamma) ** 2
- alpha * gamma**2
+ beta * (k2 - delta) ** 2
- beta * delta**2
+ 2
)
q1_fact
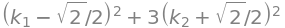
expand(q1_fact)
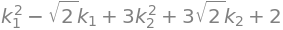
expand(q1_fact) == q1
True
We see that the above listed four constants give us the wanted factorized form from the problem text, which is a correct factorization of
(d)#
We are informed that
k_statpt = Matrix([gamma, delta])
k_statpt
The point written in the original coordinates:
x_statpt = Q * k_statpt
x_statpt
The Hessian matrix of
Exercise 5#
Given parametrization of a solid region, for
def r(u, v, w):
return Matrix([v * u**2 * cos(w), v * u**2 * sin(w), u])
u, v, w = symbols("u v w")
r(u, v, w)
We note that
(a)#
Plotting the region:
from sympy.plotting import *
pa = dtuplot.plot3d_parametric_surface(
*r(u, v, w).subs(v, 1), (u, 0, 1), (w, 0, pi / 2), show=False
)
pb = dtuplot.plot3d_parametric_surface(
*r(u, v, w).subs(w, pi / 2), (u, 0, 1), (v, 0, 1), show=False
)
pc = dtuplot.plot3d_parametric_surface(
*r(u, v, w).subs(w, 0), (u, 0, 1), (v, 0, 1), show=False
)
pd = dtuplot.plot3d_parametric_surface(
*r(u, v, w).subs(u, 1),
(v, 0, 1),
(w, 0, pi / 2),
{"color": "royalblue", "alpha": 0.7},
show=False
)
(pa + pb + pc + pd).show()
The Jacobian matrix:
Jac_mat = Matrix.hstack(diff(r(u, v, w), u), diff(
r(u, v, w), v), diff(r(u, v, w), w))
Jac_mat
The Jacobian determinant:
Jac_det = simplify(Jac_mat.det())
Jac_det
(b)#
Given vector field:
x, y, z = symbols("x y z")
V = Matrix([x + exp(y * z), 2 * y - exp(x * z), 3 * z + exp(x * y)])
V
Given function:
f = Lambda(tuple((x, y, z)), diff(V[0], x) + diff(V[1], y) + diff(V[2], z))
f(x, y, z)
(c)#
We see above that
(d)#
Since
integrate(f(*r(u, v, w)) * abs(Jac_det), (u, 0, 1), (v, 0, 1), (w, 0, pi / 2))
Exercise 6#
Given elevated surface:
def h(x, y):
return 2 * x - y + 1
x, y = symbols("x y")
h(x, y)
(a)#
Parametrisation of
r = Lambda(tuple((u, v)), Matrix([u, v, h(u, v)]))
u, v = symbols("u v")
r(u, v)
wich parameter intervals
plot3d_parametric_surface(*r(u, v), (u, 0, 2), (v, 0, 1))
Normal vector to the surface:
N = diff(r(u, v), u).cross(diff(r(u, v), v))
N
The Jacobian function in case of surface integrals is the length (norm) of the normal vector:
Jac = N.norm()
Jac
The area of
integrate(Jac, (u, 0, 2), (v, 0, 1))
(b)#
The region is now cut in two by a vertical plane through the points
s = Matrix([u, (1 - u/2) * v])
s
The elevated surface above
r1 = Lambda(tuple((u, v)), Matrix([*s, h(*s)]))
r1(u, v)
Plot:
plot3d_parametric_surface(*r1(u, v), (u, 0, 2), (v, 0, 1))
Normal vector:
N1 = simplify(diff(r1(u, v), u).cross(diff(r1(u, v), v)))
N1
The Jacobian function:
simplify(N1.norm())
Since
Jac1 = -sqrt(6) * (u - 2)/2
Jac1
(c)#
Given function
def f(x, y, z):
return x + y + z - 1
f(x, y, z)
Surface integral of
integrate(f(*r1(u, v)) * Jac1, (u, 0, 2), (v, 0, 1))
